You’ve already heard me complain about data quality — how it’s a bigger problem than most people realize, and a harder problem than many people hope. But let’s not leave it there! Perfect datasets mostly exist in textbooks and computer simulations. We need to figure out what we can do with what we have. In this and other posts, I hope to give the developers in our community some idea of how they can deal with less-than-perfect data.

The first step is to figure out how bad things actually are. To do that, we’ll use some simple statistics — those of you with a strong stat background can skip to the next entry in your RSS reader (or better yet, correct my mistakes in comments).

The GAO provides a good example of how to tackle this kind of problem. They were asked to examine government spending on the nonprofit sector — a process that ultimately led to this report (PDF). As you might imagine, there are a number of ways that federal dollars make their way to nonprofits, from loan guarantees to tax breaks to medicare payments to nonprofit hospitals. For the most part, each of these is tracked through a distinct system.

Let’s confine our work to one of the systems that GAO examined: the Federal Award and Assistance Data System, or FAADS. Along with FPDS, this makes up one half of the data powering USASpending.gov. FAADS tracks grant payments (and some other things that we’ll ignore for now). Let’s just examine that question: how do we figure out how much federal grant money went to nonprofits?

First we should define the subset of FAADS that deals with the nonprofit sector. If we can do that, and there aren’t any other problems, then we should be able to just sum up the records and figure out the totals. There’s a fairly obvious way to do this: FAADS records have a “recipient type” multiple-choice field, and one of the possible values is “nonprofit”. But of course it’s not actually that simple: the full name for the value is “other nonprofit”. The field’s possible values also include “private higher education”. If you take a quick look at some records with that value, you’ll see that many of those educational institutions are nonprofits. Worse, a look at the “nonprofit” category shows some suspicious entries. It’s worth taking a closer look at the reliability of the values entered into this field.

But we need to get beyond saying the data is “pretty good” or “kind of dodgy” or “really bad”. It would be useful to come up with a quantified estimate of how reliable the field is. GAO did this by picking a random sample of records, then checking each one to see whether it was correctly classified. That gave them a precise answer about how good the classification was within the sample — but what does the quality of the sample tell us about the quality of the larger dataset? To figure this out, GAO calculated the confidence interval of their result.

The idea is pretty simple. Let’s say there’s a big population out there, and you want to quantify some attribute of it. Unfortunately, it’s not practical to examine that value for every member the population. Instead, you’ll take a smaller sample of the population, finding the value of the attribute just for its members. How close will that value be to the real value you’d get if you did examine the entire population? It’s impossible to say for sure, but thanks to the magic of the Central Limit Theorem, we can look at how erratic the sample’s values are and get an estimate of just how good it is at representing the larger population.

You’ve probably run into confidence intervals before when reading about political polls. “Politician A has a 50% favorability rating, +/- 3 points!” This means that the pollsters are 95% confident that the real favorability rating — the one they’d get if they asked every relevant person — is between 47% and 53%. Why are they 95% sure of this, instead of 90% or 99%? Well, 95% is a natural number to use thanks to the properties of the normal distribution, but in truth it’s a bit arbitrary — it’s just sort of the stat-industry standard (interestingly, this means that one out of every twenty statistically significant results will be specious, even if the experimenters made no mistakes — something to keep in mind the next time you read a breathless account of some amazing just-published scientific discovery).

As you might imagine, for a given population there are a few factors that can be tweaked when evaluating the confidence interval: sample size, confidence level, and the width of the confidence interval. As already mentioned, that second term is generally held constant at 95%; but tradeoffs are often made between the other two. You can get a more precise confidence interval by increasing your sample size, for example — but that usually costs time or money.

But let’s get back to the nonprofit problem. The GAO took a random sample of records from the “nonprofit” category and a random sample of all the other records in FAADS. They then turned to whatever supplementary sources they could lay their hands on to figure out if the listed recipient for each record was actually a nonprofit — they used the IRS Business Master File, the Census of Governments, the Higher Education Directory, and various other subject-specific guides to the nonprofits present within specific economic sectors.

There were three possible results to each examination for a recipient’s true nonprofit status: it could be a nonprofit, or not a nonprofit, or the investigation could be inconclusive. After examining the samples, they had a percentage value attached to each of these outcomes, which represented each outcome’s share of the sample.

Each of those values can then plugged into this formula:

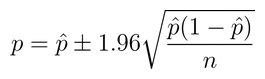
Where p is the true share of the population that falls within the category (e.g. “is a nonprofit” or “uncertain”), n is the size of the sample, and the p with a hat (called “p-hat”, pleasantly enough) is the observed proportion of the sample falling in the category.

Simple! There are a number of assumptions underlying this which hide the statistical machinery: the assumption of equivalence between the standard deviation of the population and that of the sample; the fact that we’re after a 95% confidence level. But this is a pretty standard way of going about it, and it seems to be how GAO approached the problem. For the nonprofit category, they reported a confidence interval of (.60-.79), meaning that about 70% of the sample turned out to represent genuine nonprofits, and based upon this they could be 95% sure that the true proportion of nonprofits in the larger population fell between 60% and 79%. They did the same thing with educational institutions, testing how many were nonprofits, and found an interval of (.88-.98).

(Some of you might have noticed that this operation can work backwards: some simple algebra reveals that GAO investigated 89 records in order to get these figures. In fact, the report says that they examined 96. This discrepancy is no doubt partly the result of rounding errors, but it’s also probably somewhat attributable to their use of a t distribution, a technique invented at the Guinness Brewery in 1908 to help make reliable predictions even when the sample size is pretty small. It’s not worth getting into the specifics here, but the upshot is that we need to adjust that 1.96 value for low values of n.)

So what can we do with this knowledge? It’s tempting to say, “Okay, we have a statistically justified range for how many of these records are correctly classified as nonprofits. Let’s take the total dollars for that category, multiply it by the high and low end of the confidence interval, and get an estimated range for total grant spending going to nonprofits.”

I wouldn’t say this is a bad idea, exactly. Certainly this gets you closer to the truth than simply taking FAADS at its word. You ought to add in the weighted sum for the educational institution category too, of course. And you should probably do the same thing for all the other recipient categories, to see how many nonprofits have been miscoded into those buckets. And it would be a good idea to account for that “unknown” category, too — the records that might or might not be nonprofits.

But even then, we’re in dangerous territory if we assume we have an answer. Much of what you read about statistics will be prefaced with “for a random variable” — when we can’t satisfy that assumption, things kind of fall apart. For instance: what if the government is in the habit of giving differently-sized grants to nonprofit recipients versus other recipients? That’s something we should test for before we just blindly weight the sum of all grants. Worse: what if we’re missing some records from the population? None of the above calculation tells us anything about anything other than the data we have in hand.

In the end, GAO didn’t pursue these lines of inquiry. Testing the nonprofit classification left things close enough for government work, as they say. Still, by examining the quality of that classification, GAO peeled back and refined one assumption, and in the process, arrived at a better estimate. Not a perfect one — there are still a number of assumptions being made here, and they’re worth examining, too. But they did get an estimate of how useful one aspect of their data was, and that’s a very good thing to know.